رفتار ساختارهای ساده و معادلات متغیرهای نرخ
رفتار سیستمهای خطی درجه اول
- «درجه» یک سیستم یا یک حلقه بسته، تعداد متغیرهای حالت موجود در آن است.
- یک سیستم یا حلقه بسته «درجه اول» فقط «یک متغیر حالت» دارد.
- سیستمهای خطی، سیستمهایی هستند که در آنها معادلات متغیرهای نرخ، به صورت «روابط خطی» بین متغیرهای حالت و متغیرهای خارجی تعریف میشوند.
-
«روابط خطی» صرفا شامل عملگر بعلاوه «+» و ضرب «x» به صورت مجموع موزون متغیرها است:
- مقدار متغیر نرخ = aS+bU
- که در آن a و b ضرایب وزنی، S مقدار متغیر حالت و U مقدار یک متغیر خارجی است.
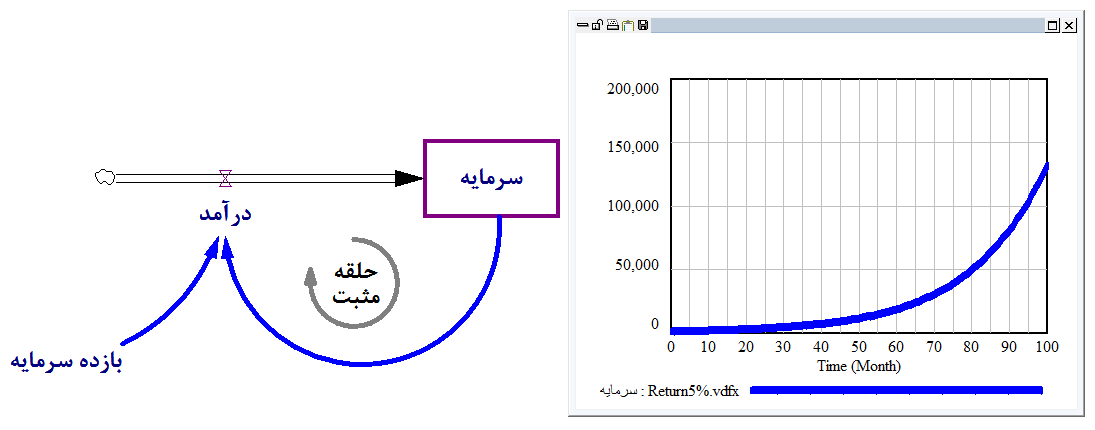
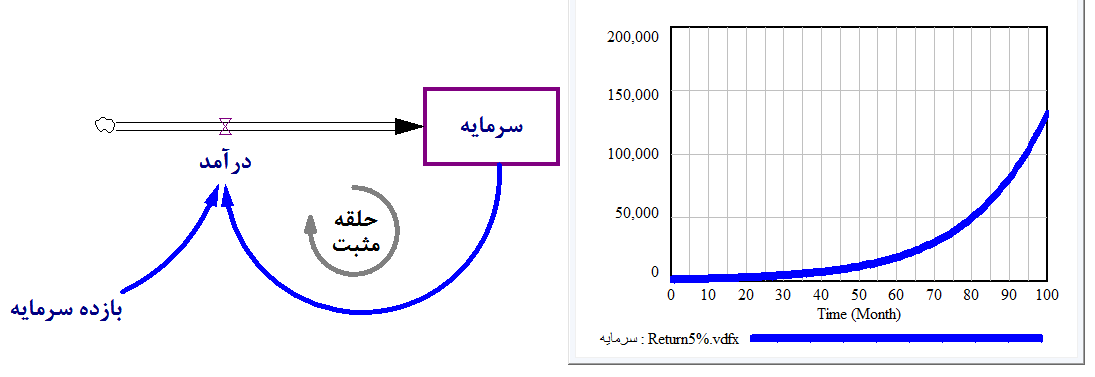
حلقه بازخوردی مثبت و رشد نمایی
- فرض کنیم یک متغیر حالت وجود دارد که توسط یک نرخ ورودی در آن انباشت ایجاد میشود.
- فرض کنیم که این متغیر حالت، بر متغیر نرخ خود اثر افزایشی دارد.
-
نتیجه این ساختار این است که «روند» رشد نمایی در متغیر حالت به وجود میآید.
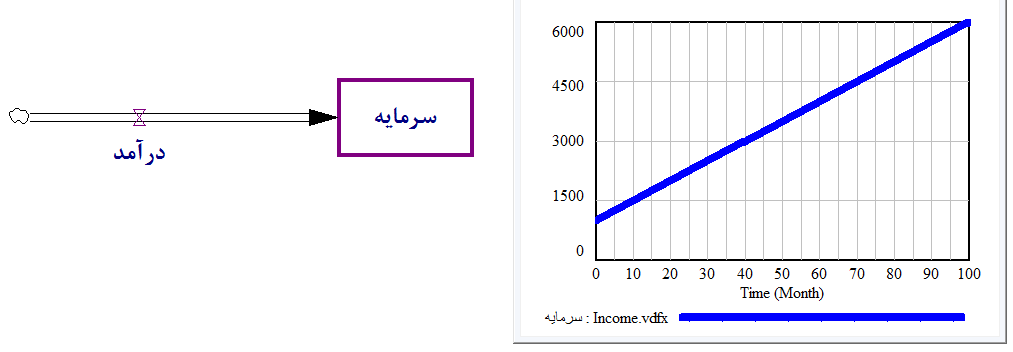
مقایسه رشد با مقدار ثابت با رشد نمایی
قدرت رشد نمایی
- رشد نمایی متغیر مورد نظر را در بازههای زمانی یکسانی «دو برابر» میکند.
- «زمان دو برابر شدن» از رابطه تقریبی 70/100g قابل محاسبه است که در آن g ضریب رشد بر حسب درصد است.
- به عنوان مثال، اگر ضریب رشد جمعیت کمی بیش از سه و نیم درصد باشد، حدود ۲۰ سال طول میکشد تا جمعیت دو برابر شود.
- یک جمعیت ۱ میلیون نفره، به این ترتیب ۲۰ سال طول میکشد تا به ۲ میلیون نفر افزایش پیدا کند.
- به همین ترتیب، پس از ۱۰۰ سال این جمعیت به ۳۲ میلیون نفر خواهد رسید.
- در ۱۰۰ سال بعد، رشد جمعیت ۹۹۲ میلیون نفر خواهد بود و به بیش از یک میلیارد نفر خواهد رسید.
- پس از ۴۰۰ سال جمعیت به بیش از ۱۰۰۰ میلیارد نفر میرسد.
- و پس از ۱۰۰۰ سال چنین رشدی جمعیت را به بیش از ۱۰۰۰ میلیارد میلیارد نفر خواهد رساند که معادل تراکم بیش از ۲ میلیون نفر بر هر متر مربع از سطح کره زمین است.
افسانه دانه گندم و صفحه شطرنج
- پادشاه به فردی که شطرنج را اختراع کرد گفت هر پاداشی که میخواهد بگوید.
- آن فرد درخواست کرد تا یک صفحه شطرنج بیاورند و گفت به ازای خانه اول ۱ گندم، به ازای خانه دوم ۲ گندم، به ازای خانه سوم ۴ گندم و بدین ترتیب به ازای هر خانه دو برابر قبلی گندم به او پاداش داده شود.
- پادشاه که فکر میکرد درخواست او ناچیز است فرمان داد سریعاً پاداش او را تهیه کنند.
- اما در واقع با محاسبه معلوم شد تهیه آن از عهده هیچ کسی بر نمیآید.
- امروزه تولید گندم کل دنیا نزدیک به ۶۰۰ میلیون تن در سال است در حالی که در مساله قبل، برای پر کردن خانه ۶۴ شطرنج به ۱۰ میلیارد تن گندم نیاز خواهد بود.
- به عنوان یک تقریب ذهنی دیگر: تعداد بازیهای شطرنجی که ممکن است انجام شود، از اتمهای کل جهان قابل مشاهده بیشتر است.
فهم رشد نمایی برای ذهن انسان سخت است
- مطالعات متعددی نشان میدهد که ذهن انسان تمایل دارد رشد را به صورت خطی درک کند.
- به این ترتیب فهم رشد نمایی برای ذهن سخت است و بدون محاسبات ریاضی، ذهن خطای زیادی در تخمینهای سرانگشتی رشد نمایی خواهد داشت.
- نتیجه این خطا این است که وقتی افراد با یک رشد نمایی مواجه هستند، تصورشان این میشود که در بازههای زمانی پایانی، ساختار متفاوتی از گذشته در سیستم شکل گرفته است که مقدار متغیر را تا این حد رشد داده است.
- علاوه بر این، لازم است توجه کنیم که رشد نمایی نمیتواند تا ابد ادامه پیدا کند.
- در دنیای محدود، دیر یا زود محدودیتی مانع از تداوم رشد نمایی خواهد شد.
- چنین محدودیتی خود را به صورت یک حلقه بازخوردی منفی نشان خواهد داد.
حلقه بازخوردی منفی و رفتار هدفجو
- فرض کنیم یک متغیر حالت وجود دارد که توسط یک نرخ ورودی در آن تغییر ایجاد میشود.
- فرض کنیم که مقدار این متغیر حالت (وضعیت فعلی)، با یک مقدار هدف مقایسه میشود و اختلاف این دو، میزان اقدام به تغییر (متغیر نرخ) را مشخص میکند.
-
نتیجه، تغییر «وضعیت سیستم» (متغیر حالت) به سمت «هدف» در یک روند «نمایی منفی» است.
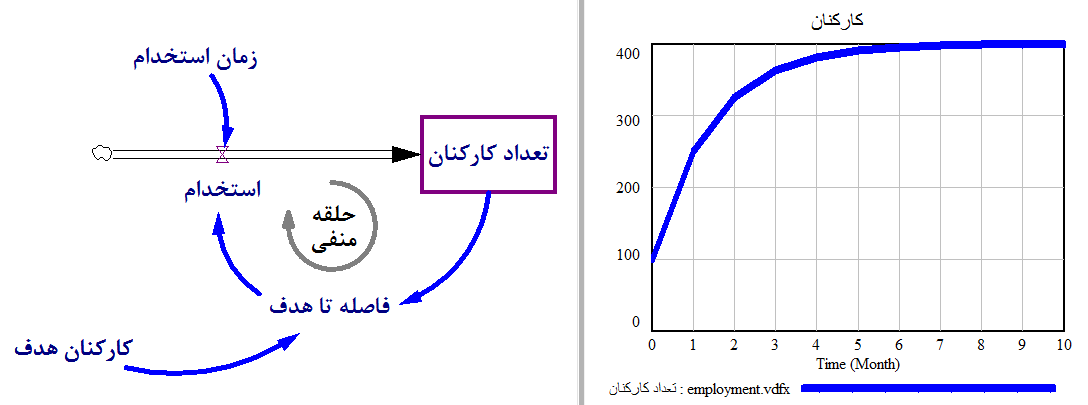
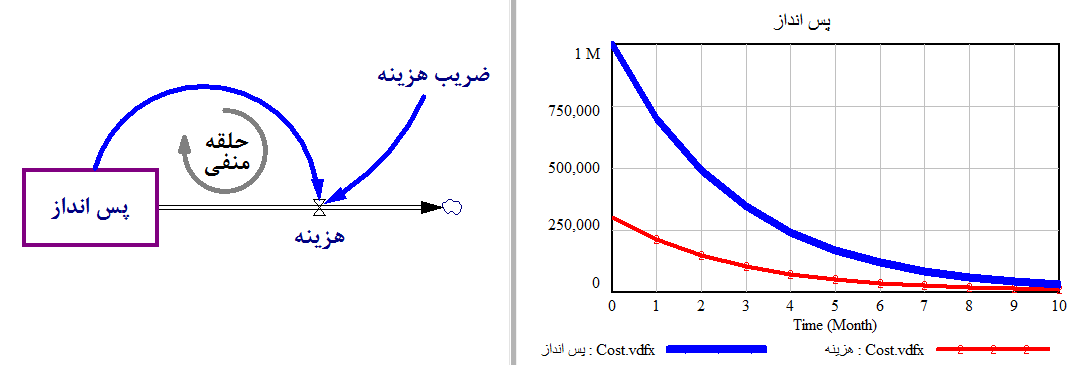
رابطه پس انداز و هزینه در یک حلقه منفی
- فرض کنیم فردی تصمیم میگیرد هر ماه به اندازه ۳۰ درصد از پس انداز خود هزینه کند.
-
اگر این فرد در این مدت درآمدی نداشته باشد، نتیجه از بین رفتن پس انداز او در یک روند نمایی منفی خواهد بود.

زمان اقدام اصلاحی در حلقه بازخوردی منفی
- حلقههای بازخوردی منفی معمولا دارای یک «هدف» هستند.
- این «هدف» با «وضع موجود» مقایسه میشود و به این ترتیب مفهوم «فاصله هدف با وضع موجود» شکل میگیرد که نیاز به «اقدام اصلاحی» دارد.
- «اقدام اصلاحی» همان متغیر نرخ است. اینکه مقدار متغیر نرخ چقدر باشد به این بستگی دارد که چقدر طول میکشد تا اقدام اصلاحی انجام شود.
- مقدار اقدام اصلاحی (متغیر نرخ) در هر مرحله حاصل تقسیم «فاصله هدف با وضع موجود» بر «زمان اقدام اصلاحی» است.
- به این ترتیب، در هر بازه زمانی معادل «زمان اقدام اصلاحی» تقریبا ۶۳ درصد «فاصله هدف با وضع موجود» جبران خواهد شد و ۳۷ درصد فاصله باقی خواهد ماند (معادل e به توان منهای یک).
- توجه به این نکته مهم است که «فاصله هدف با وضع موجود» در «زمان اقدام اصلاحی» کاملا از بین نمیرود زیرا در حلقه منفی، نرخ تغییر ثابت نیست و در هر مرحله کمتر میشود.
روند «نمایی منفی» و مفهوم «نیمه عمر»
- همانطور که منحنی رشد نمایی دارای «زمان دو برابر شدن» است، منحنی نمایی منفی دارای «نیمه عمر» است.
- «نیمه عمر» دوره زمانی است که طی آن، مقدار متغیر حالت «نصف» مقدار اولیه میشود.
- «نیمه عمر» هم از رابطه تقریبی 70/100d قابل محاسبه است که در آن d ضریب تغییر بر حسب درصد است.
اتصال حلقهها به یکدیگر
- در دنیای واقع معمولا چندین حلقه در تعامل با هم رفتار سیستم را مشخص میکنند.
- در ساده ترین حالت میتوانیم اتصال یک حلقه منفی به یک حلقه مثبت را در نظر بگیریم که هر دو حلقه به صورت خطی تغییر میکنند و به یک متغیر حالت متصل هستند.
-
در این صورت سه رفتار برای متغیر حالت قابل تصور خواهد بود:
- حلقهها متعادل هستند: نرخ ورود و خروج برابر هستند و مقدار متغیر حالت ثابت میماند.
- حلقه مثبت غالب است: نرخ ورود بیشتر از نرخ خروج است و رفتار سیستم رشد نمایی است.
- حلقه منفی غالب است: نرخ خروج بیشتر از نرخ ورود است و رفتار سیستم هدفجو است.
سه رفتار در متغیر حالت بر حسب مقدار ورودی و خروجی
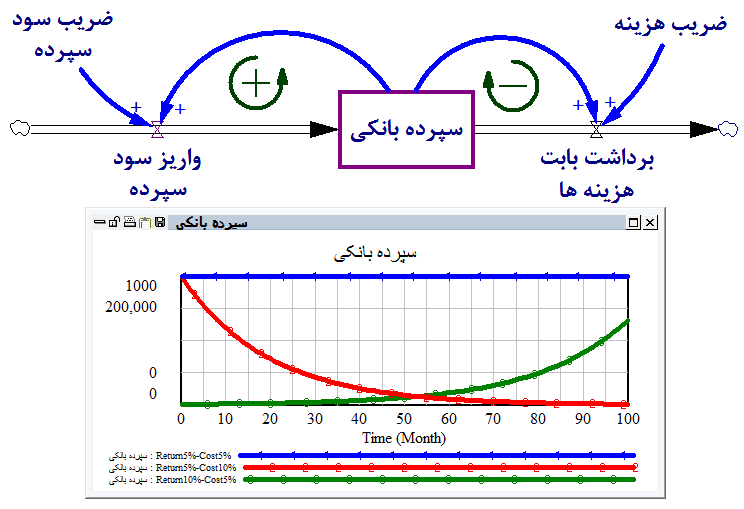
حلقههای مثبت و منفی و رفتار جمعیت
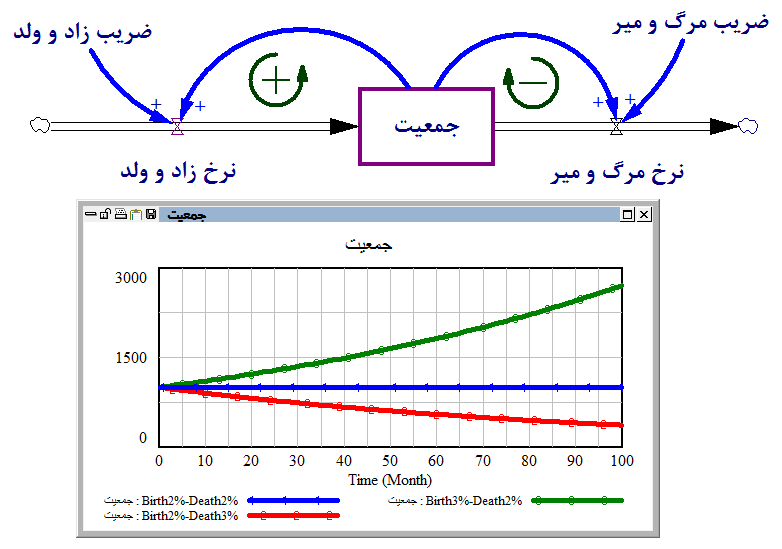
روابط غیر خطی در متغیرهای نرخ جمعیت
در پناه خدا باشیم
Previous
Next